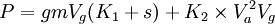Cycling Calories Algorithm

I want to add a calories burned calculation to MassUp.us plots.

It already knows distance and speed, so it could be easy given just weight and gender. This would appear on plots, for example see http://massup.us/ccm/r and click Options.

 

I could see a complete solution using wind and incline, speed and weight, age and gender, intensity and fitness, but simpler is good.  I've seen it as simple as 0.28kc/mi/lb, but would like to at least add a speed factor value, which is...? (probably a square of something)

 

I figured maybe someone here knows a good cycling calories algorithm or has a best reference.  Google gives too much, with little agreement, and mostly forms and tables rather than equations, so hoping for human input...

 

If nobody here knows with certainty, would someone like to figure it out please?

 

Views: 4204

▶ Reply to This

Replies to This Discussion

Permalink Reply by S on October 15, 2011 at 5:43am

I think the reason why you can't find a simple equation is that it's not as easy as you think.  There's a lot more factors than just speed, distance, and weight.  The wind plays an important part and a lot of that depends on how windy things are, where you are in relation to others (being in the middle of a peloton can drop your power requirements by 60+%). 

 

That being said check this page out for a discussion of the various forces and factors.  Their model gives you the power requirements which when combined with the time spent riding gives you the energy used. You can take their model and make simplifying assumptions but you really need to be careful not to oversimplify and get results that don't give meaningful information.  E.g. if the wind speed values are off from your assumption, then the result could be 100 or more calories off from the actual energy expenditure. 

 

Ultimately, I think the results are sensitive enough to factors that can vary between individuals that any calculations are probably going to be sort of wrong to totally wrong. Just find a somewhat convenient equation to use, then tell people that result might be as much 100-200 calories off from what they actually burned.

Permalink Reply by Andrew Bedno on October 15, 2011 at 7:25am

Perfect!  http://www.analyticcycling.com/ForcesPower_Page.html

 

Part of why some of what can be found is in table form I think is because there's been good labs giving point samples, but they don't easily reduce to a simple function.

So distance and weight are primary (0.28kc/mi/lb), then speed and headwind. Incline and altitude I'm gonna ignore for now thanx to Chicago being flat. Intensity and fitness are hard to quantify. Age and gender I suppose are moot?

A next good target then would be to also take a stab at calculating the margin of error.  Or I'll just put "for entertainment purposes only"

So I need the function that integrates speed and headwind, which is over my head. C'mon math geeks...

Permalink Reply by Andrew Bedno on October 17, 2011 at 8:55am

http://en.wikipedia.org/wiki/Bicycle_performance

P = g m V_g (K_1+s) + K_2 \times V_a^2 V_g

Where P is in watts, g is Earth's gravity, Vg is ground speed (m/s), m is bike/rider mass in kg, s is the grade (m/m), and Va is the rider's speed through the air (m/s). K1 is a lumped constant for all frictional losses (tires, bearings, chain), and is generally reported with a value of 0.0053. K2 is a lumped constant for aerodynamic drag and is generally reported with a value of 0.185 kg/m.

Substituting some constants:

calories =  ((9.8*weight*speed*(0.0053+1))+(0.185*wind^2*speed))*1.16*hours


(draft candidate equation, I may have gotten it grossly wrong, gonna add metric/english conversion and run some trial curves to sanity check)

Permalink Reply by Mike Zumwalt on October 17, 2011 at 12:53pm

This is over my head but a head wind/tail wind or cross wind will make a big difference.

Something like heading INTO a 15 mph wind while pedaling at 15 mph is the equivalent of doing 30 mph and may be even harder on the legs as the rolling speed is not actually 30 mph but 15.

Permalink Reply by Andrew Bedno on October 17, 2011 at 2:26pm

The wikipedia article is good, and acknowledges wind as the hardest element to incorporate, their main arguments being about measuring.  My draft doesn't adequately factor in wind direction. Gonna think about that... I may simplify to head/tail:hi/med/low/none

 

Some interesting lessons in this for me have been that bikes are EXTREMELY efficient, which simplifies calculations, and the biggest loss is aerodynamic drag.

Permalink Reply by S on October 17, 2011 at 4:37pm
The other important factor with the wind is your position in the mass.  Someone riding in the center of the group is not going to see any wind unless there are hurricane force winds around and someone at the edge or front is going to see a lot or all of it.  The wind speeds in the forecasts are also measured in unobstructed places and don't take into account the effects of buildings and other structures.  Long and short, I'd just assume Va = Vg and call it a day.  It'll effect your results but you're only trying to get a rough figure anyway so it won't matter much.  Anyone that cares is going to have a power meter and have figures accurate to 3-5%.
Permalink Reply by Andrew Bedno on March 1, 2012 at 3:48pm

Because I enjoy finishing things, here's the cycling calorie figures I used following this discussion.  Any plot on MassUp.us now shows approximate burn.  After much study, simply using a difficulty selector (vs factoring speed, direction, incline, drag...) seemed an adequate approach.

Calories per mile per pound:

Gentle ride=0.26
Biking=0.29
Moderate ride=0.31
Hard ride=0.35
Walking=0.53
Jogging=0.64
Running=0.75
Gentle Skating=0.34
Moderate Skating=0.42
Hard Skating=0.5
Driving=0

Permalink Reply by Yasmeen on February 3, 2016 at 3:42am

This looks like a good chart for figuring out calories burned. Did you find this on a website? (It's been a while since you posted it but I figured I'd ask). :-)

Permalink Reply by Andrew Bedno on February 3, 2016 at 6:30am

Thanks!  That quick list is as described, the results of this thread's research. A compromise solution good enough to use in software.

I later verified these figures closely match those used in some popular fitness programs.

Permalink Reply by Andrew Bedno on February 3, 2016 at 6:34am

Another view, from least to most efficient per mile:

0.75 Running
0.64 Jogging
0.53 Walking
0.50 Hard Skating
0.42 Moderate Skating
0.35 Hard ride
0.34 Gentle Skating
0.31 Moderate ride
0.29 Biking
0.26 Gentle ride

Seems to indicate biking is more than twice as efficient as walking (and three times running) in calories/mile.  I'd have expected more.

Permalink Reply by Ride it like you stole it on March 2, 2012 at 4:35am
Permalink Reply by Jeff Blumenthal on March 2, 2012 at 7:52am

All I know from physics is that Energy and Work are equivalent and Work = Force x Distance.  Force is proportional to speed through the air, so wind is important.  Speed or velocity is Distance divided by time, so you have Energy ~ k (Distance)^2 / Time or Energy ~ k Time x (Velocity)^2.

Since wind is involved I'll go with the second form using the square of velocity.

k = some kind of constant ...

Now I'm lost...

RSS

Groups

© 2008-2016   The Chainlink Community, L.L.C.   Powered by

Disclaimer  |  Report an Issue  |  Terms of Service